Package Design Guide
- Introduction
- Determine Product Fragility
- Determine Conditions
- Calculate Cushion Requirements
- Recognizing Design Constraints
- Design Prototypes and Test
- Consider Vibration Effects
- Monitor Performance
Package Design Guide
STEP THREE: Calculate Fundamental Cushion Requirements
When product fragility (g-factor) and handling environment (drop height) have been determined, the procedure that follows can be used to determine the amount of functional cushioning material which will provide adequate protection for the packaged item.
By functional cushioning material, we mean that portion of the design which directly supports the load and functions to absorb shock during impacts. There may be additional material used in the design as well to connect functional cushioning parts together, facilitate pack assembly, etc. This procedure does not take into account such factors as the effect of the outer container or other effects that may take place inside the container.
Generally such effects are beneficial so that this procedure can confidently be used as a starting point to develop packaging that provides an assured level of protection and optimum cost-efficiency. To calculate functional cushioning needs it will be necessary to understand and use dynamic cushioning curves.
Using Dynamic Cushioning Curves: An Overview
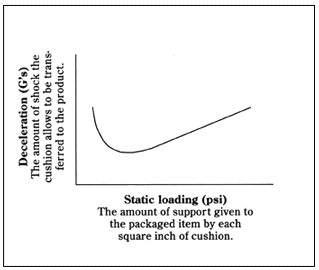 |
| Typical dynamic cushioning curve |
A cushioning curve shows how a particular packaging material of a given thickness behaves at different impact conditions. Curves are generated by dropping a series of known weights onto a cushion sample from a specified height and measuring the amount of shock experienced by the weights as they impact the foam. In simple terms, this testing represents a product dropping on a cushion from a height likely to be encountered during shipment.
An idealized cushioning curve is shown below. It represents the cushioning performance of a cushioning material for a given combination of thickness and drop height. The horizontal axis represents a range of static loadings (in pounds per square inch) that packaged items might apply to the cushioning material. The vertical axis represents the shock experienced as the cushion is impacted. Curves are often presented for both first impact and multiple impact (average of drops 2-5) data. It is common to include data for several cushion thicknesses from a constant drop height on a single set of axes.
Cushioning curves for ETHAFOAM* products may be obtained by contacting your local Dow-authorized fabricator, your local Dow representative, or Dow’s Research and Development facility.
Using Dynamic Cushioning Curves:
An Example
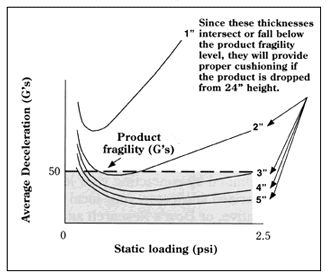 |
| Determining Cushion Thickness 24" drop height, 2-5 drop average |
An object to be packaged is a 10-inch cube weighing 60 pounds with a fragility of 50 g’s. Since a product typically faces repeated impacts during shipment, you will probably wish to use multiple-impact data. The typical drop height for a product of this weight may be estimated from the chart below as 24 inches, however specific knowledge of shipping conditions or corporate standards may dictate a different choice for drop height.
First, obtain the cushioning curves for the cushioning material you wish to use. Locate curves that represent multiple impact data from a drop height of 24 inches. One such set of curves is shown here.
Determining Thickness
Using the chart below as a reference, locate our product’s fragility level (50 g’s) on the vertical axis of the figure, and draw an imaginary horizontal line across the chart at this level.
This separates the chart into two sections:
- our fragility line and lower, where the packaged item will be able to survive the anticipated shock level, and
- the section above our line where the shock levels are high enough to damage the product
Note that in this example, a 1-inch thickness of this cushioning material will not protect the item down to 50 g’s because the entire 1-inch curve is located above the 50 g line, in the "damage" zone. All of the other curves, representing cushions 2 inches thick and greater, have portions down in the "no damage" zone, and thus can be used. In most cases, shipping and handling considerations provide a strong cost incentive to design as small a package size as possible, so the thinnest cushion thickness which will do the job is most often selected. In this case, we will choose a thickness of 2 inches.
Determining Static Loading and Bearing Area
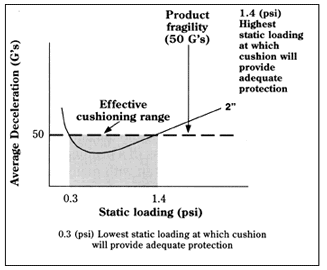 |
| Determining Static Loading Range 24" drop height, 2-5 drop average |
Only a portion of the 2-inch cushion curve can be used to protect our product to 50 g’s. As seen below, the useable part of the curve is bounded by a static loading of 0.3 psi at the low end, and 1.4 psi at the high end. This tells us that, with a 2-inch cushion, we can apply a static loading anywhere within this "cushioning range" and still protect to 50 g’s or lower.
We now must choose a static loading to use within this range and design our cushions. The highest static loading value within the cushioning range will result in the most economical design because it will use less cushioning material to provide adequate protection, thus lowering design costs. Continuing with our example will illustrate how.
Once we have selected a static loading, we can calculate how many square inches of foam in our chosen thickness we’ll need to support and protect any side of the packaged product. In most cases it will be necessary to design a cushion to protect each of the faces of the product.
The cushion bearing area is easily calculated as the product weight divided by our chosen static loading. In this example, we have an allowable static loading range of 0.3 to 1.4 psi. If we were to choose to design with a static loading at the lower end of our range, 0.3 psi, we would divide our 60 pound product weight by 0.3 psi and find that we would need to support our product with 200 square inches of foam to produce a design which loads the foam to 0.3 psi.
If we were to choose the higher loading value of 1.4 psi instead, we would divide 60 pounds by 1.4 psi and find that only 43 square inches of foam are necessary to support the product at this higher loading. This is a 78.5% reduction in cushioning material compared to designing at 0.3 psi. You can imagine the cost savings that can result.
The use of higher loading values to optimize designs cannot be overemphasized. As a general rule, if you can double or triple the loading value and still not exceed your product fragility level, you can reduce your cushion usage by one-half to two-thirds. As a result, total material costs will be minimized.
Note that it may be possible to use even a smaller volume of foam by increasing thickness somewhat and taking advantage of the higher loading (and smaller bearing area) this allows. The resulting increase in shipping and handling costs due to package size increase is often greater than the saving in cushion material costs, so designing to the minimum thickness is the general practice.
By repeating this procedure with several materials, you can quickly generate comparisons, which will allow you to strike an economical balance between material cost and package size.